

It is possible to predictively evolve the q profile (and by extension the current profile and poloidal field) using the poloidal field diffusion equation. In this case it is unnecessary to provide time-dependent q profile data. A form of the poloidal field diffusion equation can be derived as follows using Ampere's law, Faraday's law and Ohm's law:
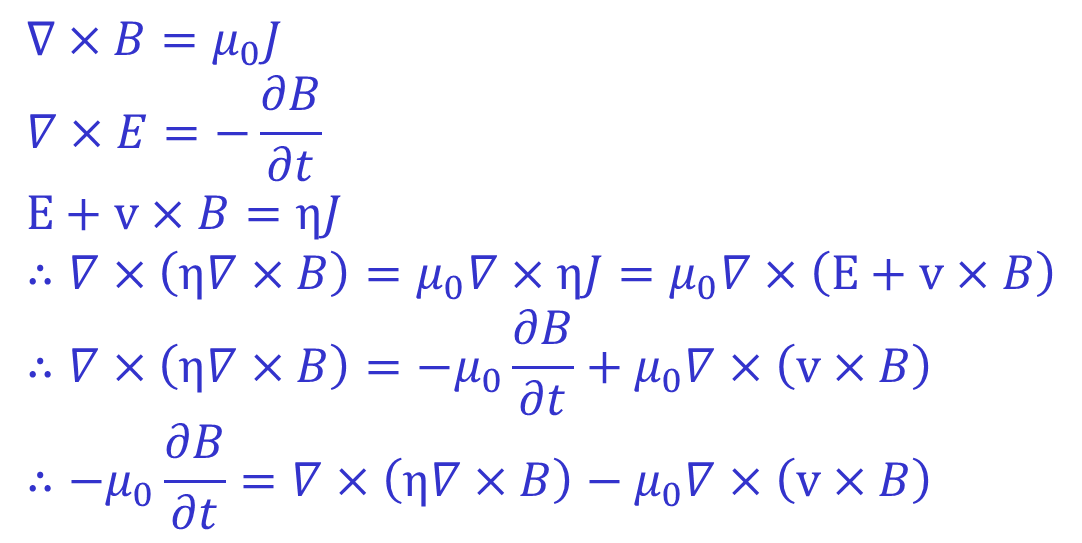
The exact variant of this equation used by TRANSP is somewhat more complicated and takes the form of a partial differential equation for the rotational transform (ι=1/q) which depends on the resistivity, the value of RBT, the non-ohmic current and a series of geometric moments of the equilibrium. This equation allows TRANSP to use the current equilibrium to advance in time the q profile as a function of toroidal flux. This is then used with the pressure to solve for the new equilibrium geometry. A more complete (although possibly somewhat dated) derivation of the form of the PFDE used in TRANSP is provided in these notes by D. McCune (in the section titled 'TRANSP 11/2 D Magnetic Field Diffusion Equation').